Расширение "Графики"
Расширение выводит графическое представление точек, заданных парами координат (x,y). Каждая пара может относиться к определённой серии данных. Точки одноимённых серий могут соединяться отрезками прямых линий, что позволяет выводить графики функций по наборам их каким-то образом табулированных значений. Расширение входит в базовую комплектацию системы и используется несколькими её расширениями.
Функция gtz() - вывод табулированных значений
Функция gtz(d[,p]) позволяет представить в графическом виде точки табулированных значений, заданных массивом d. В простейшем случае d - это двумерный массив, содержащий строки с именами "x" и "y". Строка с именем "x" должна содержать массив значений аргумента, а строка с именем "y" - значения, соответствующие данному аргументу. Далее такого типа структуру данных будем называть массив табулированных значений. Массивы табулированных значений создаются и используются несколькими расширениями системы.
Рассмотрим пример создания и использования массива табулированных значений и функции gtz().
Разметка
~d1('x')=massiv('-2 -1 0 1 2 3')
~d1('y')=massiv('-4 -2 0 2 4 6')
@gtz(d1)
Вывод
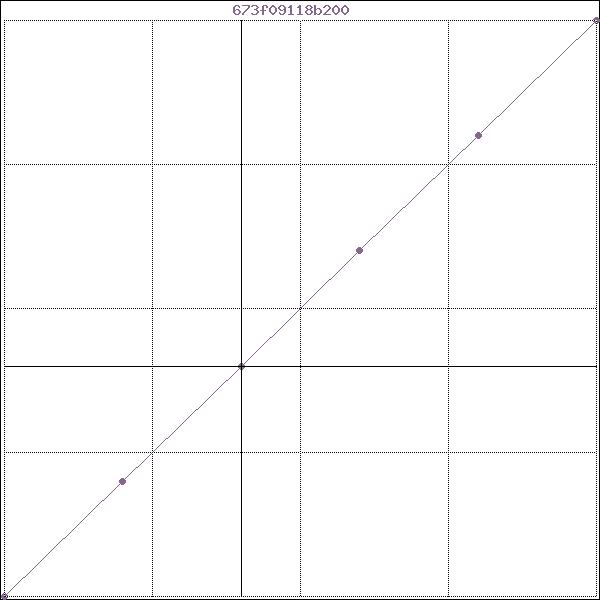
В более общей форме массив d может быть массивом массивов табулированных значений. В этом случае индексы элементов первого измерения массива d рассматриваются как имена серий, а значениями элементов такого массива должны быть массивы табулированных значений.
Разметка
~d2('x')=massiv('-2 -1 0 1 2 3')
~d2('y')=massiv('-6 -3 0 3 6 9')
~d3('x')=massiv('-2 -1 0 1 2 3')
~d3('y')=massiv('-2 1 0 1 2 1')
~d('d1')=d1
~d('d2')=d2
~d('d3')=d3
@gtz(d)
Вывод
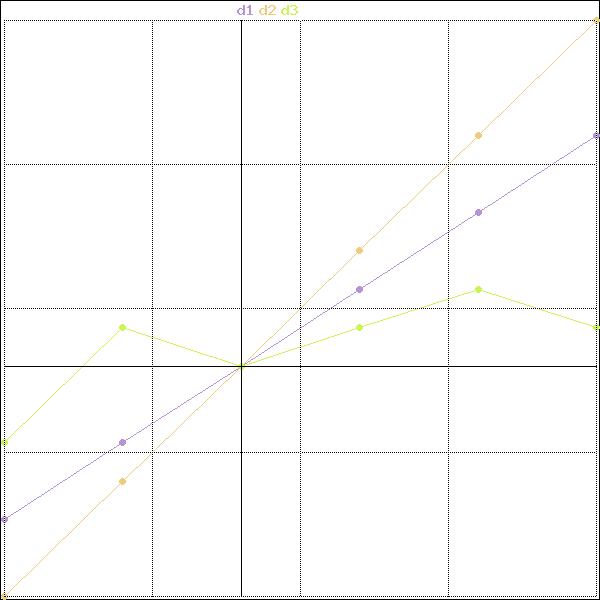
Для управления выводом графиков используются данные, задаваемые массивом или строкой p, содержащей параметры заданные в форме ключ:значение. Могут использоваться следующие параметры:
w - ширина области вывода в пикселях (по умолчанию 600);
h - высота области вывода в пикселях (по умолчанию равна w);
r - радиус точки в пикселях (по умолчанию 7);
s - признак необходимости соединения точек серий (0 - не соединять, 1 - соединять, по умолчанию);
v - число вертикальных линий разметки (по умолчанию 5);
g - число горизонтальных линий разметки (по умолчанию 5).
Параметр w определяет ширину области вывода в пикселях. Если он не задан или не является числом, то его значение равно 600. Параметр h определяет высоту области вывода в пикселях. Если он не задан или не является числом, то высота приравнивается к ширине (h=w).
Параметр s определяет надо ли соединять точки серий линиями. Если он равен нулю, то точки не соединяются. В противном случае (по умолчанию) точки серий соединяются. Обычно точки соединяются для изображения графиков функций. Но если нужно просто изобразить "облако" данных, то точки можно не соединять. Также рекомендуется не соединять точки при выводе неявных функций. см. Исследование неявных функций двух переменных.
Все точки серии и соединяющие их линии выводятся одним цветом, который выбирается случайно. Поэтому при перезагрузке страницы они всегда меняются. Если задан параметр v, то область графика разделяется на v-1 вертикальные полосы. Если задан параметр g, то область графика разделяется на g-1 горизонтальные полосы. По умолчанию v=g=5. Ось абсцисс отображается в том случае, если хотя бы в одной из секций имеются как отрицательные, так и положительные значения функций. Ось ординат отображается только тогда, когда хотя бы в одной серии имеются как положительные, так и отрицательные значения аргумента. Сверху графика выводятся идентификаторы серий, в цвете, выбранном системой для отображения графика этой серии.
Ширина и высота области вывода не являются абсолютными. Если ширина контейнера для вывода графического представления графиков меньше заданной ширины, то изображение пропорционально подгоняется под 100% его ширины.
Пошаговый вывод графиков
Более общим способом вывода графиков является пошаговый метод, при котором последовательно выполняются несколько встроенных функций расширения "Графики". Он позволяет более гибко организовать процесс построения графиков, использовать собственные цвета и регулировать размер точек для каждой серии данных, настраивать границы внутренней области представления данных, а также выводить тексты слева, справа, сверху и снизу графиков. Пошаговый метод реализуется набором функций расширения, представленных в следующей таблице.
| Функция | Назначение |
| holst | Создание холста для рисования графиков |
| gdxy | Добавить значение точки в серию |
| gdvs | Добавить вектора данных серии |
| gvtd | Вывести точки всех серий данных |
| gvts | Вывести точки серии |
| gsts | Соединить последовательные точки серии линиями |
| gdok | Добавить оси координат |
| gvgs | Вывести горизонтальную сетку |
| gvvs | Вывести вертикальную сетку |
| gvos | Вывести обозначения серий в заданной области |
| gvct | Вывести центрированный текст в заданной области |
| gvtv | Вывести текст вертикально в заданной области |
| gsf | Вывести изображение на холсте в заданный файл |
Функция holst()
Функция holst(p) создаёт объект "График", инициализирует его параметры и возвращает идентификатор данного объекта для последующего использования всеми прочими функциями. Она получает единственный параметр p, представляющий собой строку, содержащую необязательные параметры, заданные в форме ключ:значение и разделённые пробелами. Могут использоваться следующие параметры:
w - ширина области вывода в пикселях (по умолчанию 840);
h - высота области вывода в пикселях (по умолчанию 640);
lo - левый отступ (по умолчанию 20);
po - правый отступ (по умолчанию 20);
vo - верхний отступ (по умолчанию 20);
no - нижний отступ (по умолчанию 20);
font - номер системного шрифта для подписей (от 1 до 5, по умолчанию 5).
Отступы определяют смещения области вывода графиков от левой, правой, верхней и нижней границ области формирования изображения и используются для вывода сопровождающих графики текстов.
Функция возвращает идентификатор объекта, который должен передаваться во все последующие задействуемые при оформлении графиков функции.
Функция gdxy()
Функция gdxy(g,x,y,s) заносит данные аргумента (x) и значения функции (y) серии (s) в объект g, полученный от функции holst(). Значения координат точки (x,y) для всех серий могут передаваться в любой последовательности.
Функция gdvs()
Функция gdvs(g,x,y,s) аналогична функции gdxy() с тем отличием, что здесь x и y являются векторами, каждая пара которых определяет координаты точки одной серии s. Фактически она эквивалентна циклическому вызову функции gdxy() для каждой пары значений из векторов x и y. Как и в функции gdxy() здесь и далее, g - это идентификатор объекта "График", полученный от функции holst().
Функция gvtd()
Функция gvtd(g[,rt]) выводит на график точки всех серий данных, ранее определённых функциями gdxy() и gdvs(). Обязательным параметром является только g - идентификатор объекта "График". Второй параметр необязателен и определяет радиус круга, используемого как изображение точки. По умолчанию он равен 4 пикселям. Все точки всех серий изображаются как заполненный круг радиусом rt.
Функция gvts()
Функция gvts(g,s,[,rt[,p]]) выводит на график точки серии s, ранее определённые функциями gdxy() и gdvs(). Обязательными параметрами являются только g - идентификатор объекта "График" и s - идентификатор серии. Параметр rt определяет радиус круга, используемого как изображение точки. По умолчанию он равен 4 пикселям. Все точки серии изображаются как заполненный круг радиусом rt. Если не задан или задан неверно параметр p, то цвета точек серии устанавливаются случайно. Параметр p является строкой, содержащей данные, заданные в форме ключ:значение и разделённые пробелами. Могут использоваться следующие параметры:
r - интенсивность красного цвета [0,255];
g - интенсивность зелёного цвета [0,255];
b - интенсивность синего цвета [0,255].
Если какой-либо из параметров r,g,b опущен или задан неправильно, то его значение выбирается случайно из отрезка [0,255].
Таким образом, функция gvts() позволяет регулировать как размер всех точек каждой серии, так и их цвет. Установленный цвет запоминается и в дальнейшем используется для вывода соединительных линий и обозначения серии.
Функция gsts()
Функция gsts(g,s) соединяет прямыми линиями точки серии s на графике g. Её параметрами являются g - идентификатор объекта "График" и s - идентификатор серии. Для вывода соединительных линий используется цвет, ранее установленный при выводе точек данной серии.
Функция gdok()
Функция gdok(g) добавляет на график g оси координат. Они всегда выводятся чёрным цветом. Ось абсцисс отображается в том случае, если хотя бы в одной из серии имеются как отрицательные, так и положительные значения функций. Ось ординат отображается только тогда, когда хотя бы в одной серии имеются как положительные, так и отрицательные значения аргумента.
Функция gvgs()
Функция gvgs(g,n) выводит горизонтальную сетку - горизонтальные линии разметки области вывода графика, разделяя её на n-1 горизонтальные полосы. Сетка всегда выводится чёрным цветом в виде прерывистых линий.
Функция gvvs()
Функция gvvs(g,n) выводит вертикальную сетку - вертикальные линии разметки области вывода графика, разделяя её на n-1 вертикальные полосы. Сетка всегда выводится чёрным цветом в виде прерывистых линий.
Функция gvos()
Функция gvos(g[,k]) выводит описания (идентификаторы) серий в заданной области вывода графиков. Параметр k не обязателен и по умолчанию равен 1. Если k=1, то идентификаторы серий выводятся в области верхнего отступа холста рисования графиков (см. параметр vo функции holst), если k=2, то по центру области вывода графиков, если k=3, то в области нижнего отступа. Строка текста с обозначениями идентификаторов серий всегда выводится по центру выбранной области. Каждый идентификатор выводитcя цветом, ранее установленным функциями gvtd() или gvts().
Функция gvct()
Функция gvct(g,tekst[,k]) выводит произвольный текст tekst в заданной области вывода графиков. Параметр k не обязателен и по умолчанию равен 1. Если k=1, то текст выводится в области верхнего отступа холста рисования графиков (см. параметр vo функции holst), если k=2, то по центру области вывода графиков, если k=3, то в области нижнего отступа. Текст всегда выводится по центру выбранной области чёрным цветом. Стоит иметь ввиду, что кириллица часто может отображаться неверно.
Функция gvtv()
Функция gvtv(g,tekst[,k]) выводит произвольный текст tekst вертикально в заданной области вывода графиков. Параметр k не обязателен и по умолчанию равен 1. Если k=1, то текст выводится в области левого отступа холста рисования графиков (см. параметр lo функции holst), если k=2, то по центру области вывода графиков, если k=3, то в области правого отступа. Текст всегда выводится по центру выбранной области чёрным цветом. Стоит иметь в виду, что кириллица часто может отображаться неверно.
Функция gsf()
Функция gsf(g[,file]) выводит сформированное изображение в файл формата jpeg и возвращает его имя для последующего отображения на странице. Если параметр file не задан, то имя формируется автоматически.
Комплексный пример
Рассмотрим типовую последовательность действий по применению перечисленных функций на примере построения графиков функций sin(x) и cos(x) для заранее построенного одинакового перечня значений аргументов. Для формирования последовательности аргументов и табулирования значений функций используются встроенные функции расширения "Исследование функций одной переменной" (файл f1.php - не входит в базовый комплект поставки).
Сначала формируем массив значений аргумента с помощью функции tap(a,h,n), где:
a - начальное значение;
h - шаг изменения;
n - количество значений.
Далее, с помощью функции tvx('выражение',массив_аргументов) табулируем значения функций sin(x) и cos(x) для каждого значения аргумента. И выводим значения аргументов и функций в виде таблицы.
Следует иметь в виду, что выражение в функции tap всегда должно зависеть от переменной с именем x, а массив_аргументов не должен иметь имя x, поскольку tap "портит" переменную с этим именем, используя его в своих корыстных целях. Поэтому последовательность значений аргумента мы записываем в массив w.
Разметка
~w=tap(-pi(),0.1,100)~sin=tvx('sin(x)',w)
~cos=tvx('cos(x)',w)
@nt(1)
@st(1,'<b>x</b>',w)
@st(1,'<b>sin</b>',sin)
@st(1,'<b>cos</b>',cos)
@kt()
Вывод
| x | -3,14 |
-3,04 |
-2,94 |
-2,84 |
-2,74 |
-2,64 |
-2,54 |
-2,44 |
-2,34 |
-2,24 |
-2,14 |
-2,04 |
-1,94 |
-1,84 |
-1,74 |
-1,64 |
-1,54 |
-1,44 |
-1,34 |
-1,24 |
-1,14 |
-1,04 |
-0,942 |
-0,842 |
-0,742 |
-0,642 |
-0,542 |
-0,442 |
-0,342 |
-0,242 |
-0,142 |
-0,042 |
0,058 |
0,158 |
0,258 |
0,358 |
0,458 |
0,558 |
0,658 |
0,758 |
0,858 |
0,958 |
1,06 |
1,16 |
1,26 |
1,36 |
1,46 |
1,56 |
1,66 |
1,76 |
1,86 |
1,96 |
2,06 |
2,16 |
2,26 |
2,36 |
2,46 |
2,56 |
2,66 |
2,76 |
2,86 |
2,96 |
3,06 |
3,16 |
3,26 |
3,36 |
3,46 |
3,56 |
3,66 |
3,76 |
3,86 |
3,96 |
4,06 |
4,16 |
4,26 |
4,36 |
4,46 |
4,56 |
4,66 |
4,76 |
4,86 |
4,96 |
5,06 |
5,16 |
5,26 |
5,36 |
5,46 |
5,56 |
5,66 |
5,76 |
5,86 |
5,96 |
6,06 |
6,16 |
6,26 |
6,36 |
6,46 |
6,56 |
6,66 |
6,76 |
| sin | -0,000 |
-0,100 |
-0,199 |
-0,296 |
-0,389 |
-0,479 |
-0,565 |
-0,644 |
-0,717 |
-0,783 |
-0,841 |
-0,891 |
-0,932 |
-0,964 |
-0,985 |
-0,997 |
-1,000 |
-0,992 |
-0,974 |
-0,946 |
-0,909 |
-0,863 |
-0,808 |
-0,746 |
-0,675 |
-0,598 |
-0,516 |
-0,427 |
-0,335 |
-0,239 |
-0,141 |
-0,042 |
0,058 |
0,158 |
0,256 |
0,351 |
0,443 |
0,530 |
0,612 |
0,688 |
0,757 |
0,818 |
0,872 |
0,916 |
0,952 |
0,978 |
0,994 |
1,000 |
0,996 |
0,982 |
0,959 |
0,926 |
0,883 |
0,832 |
0,773 |
0,706 |
0,631 |
0,551 |
0,465 |
0,374 |
0,279 |
0,182 |
0,083 |
-0,017 |
-0,117 |
-0,215 |
-0,312 |
-0,405 |
-0,494 |
-0,578 |
-0,657 |
-0,729 |
-0,794 |
-0,850 |
-0,899 |
-0,938 |
-0,968 |
-0,988 |
-0,999 |
-0,999 |
-0,989 |
-0,970 |
-0,941 |
-0,902 |
-0,855 |
-0,798 |
-0,734 |
-0,663 |
-0,585 |
-0,501 |
-0,412 |
-0,319 |
-0,223 |
-0,124 |
-0,025 |
0,075 |
0,174 |
0,272 |
0,366 |
0,458 |
| cos | -1 |
-0,995 |
-0,980 |
-0,955 |
-0,921 |
-0,878 |
-0,825 |
-0,765 |
-0,697 |
-0,622 |
-0,540 |
-0,454 |
-0,362 |
-0,267 |
-0,170 |
-0,071 |
0,029 |
0,129 |
0,227 |
0,323 |
0,416 |
0,505 |
0,589 |
0,666 |
0,737 |
0,801 |
0,857 |
0,904 |
0,942 |
0,971 |
0,990 |
0,999 |
0,998 |
0,987 |
0,967 |
0,936 |
0,897 |
0,848 |
0,791 |
0,726 |
0,654 |
0,575 |
0,490 |
0,401 |
0,307 |
0,211 |
0,112 |
0,012 |
-0,087 |
-0,187 |
-0,284 |
-0,378 |
-0,469 |
-0,554 |
-0,635 |
-0,709 |
-0,776 |
-0,835 |
-0,886 |
-0,927 |
-0,960 |
-0,983 |
-0,997 |
-1,000 |
-0,993 |
-0,977 |
-0,950 |
-0,914 |
-0,869 |
-0,816 |
-0,754 |
-0,685 |
-0,608 |
-0,526 |
-0,439 |
-0,347 |
-0,251 |
-0,153 |
-0,054 |
0,046 |
0,146 |
0,244 |
0,339 |
0,431 |
0,519 |
0,602 |
0,679 |
0,749 |
0,811 |
0,865 |
0,911 |
0,948 |
0,975 |
0,992 |
1,000 |
0,997 |
0,985 |
0,962 |
0,930 |
0,889 |
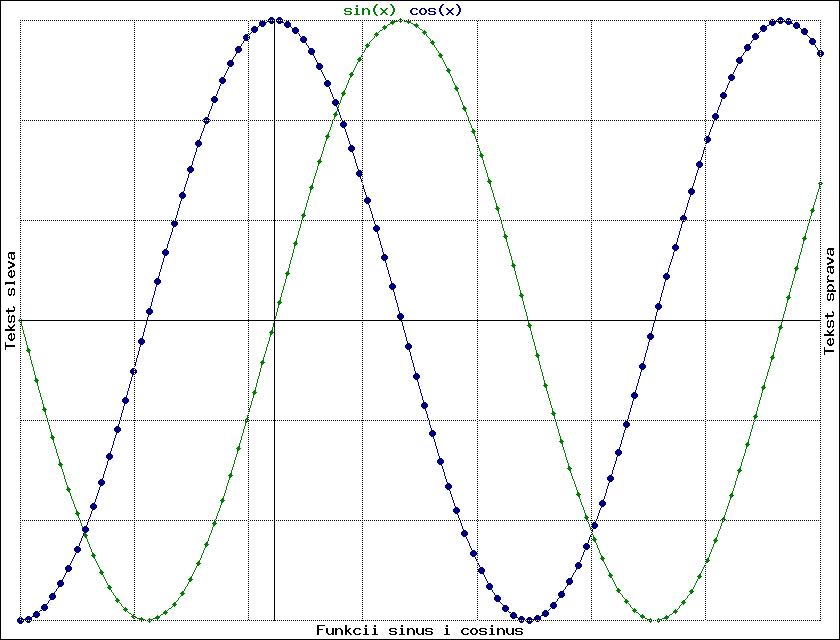
Таким образом, у нас есть значения аргумента в массиве w и соответствующие им значения искомых функций в массивах sin и cos. Теперь создаём объект "График" и переносим в него данные, присваивая сериям имена sin(x) и cos(x).
Разметка
~g=holst()@gdvs(g,w,sin,'sin(x)')
@gdvs(g,w,cos,'cos(x)')
Теперь "рисуем" на графике точки серии sin(x) "половинным" зелёным цветом, установив радиус точек в 4 пикселя и соединяем точки прямыми линиями. То же самое делаем для серии cos(x), но здесь делаем точки побольше (радиус 7 пикселей) и закрашиваем их "половинным" синим цветом.
Разметка
@gvts(g,'sin(x)',4,'r:0 g:127 b:0')@gsts(g,'sin(x)')
@gvts(g,'cos(x)',7,'r:0 g:0 b:127')
@gsts(g,'cos(x)')
Выводим сетку разметки области вывода графика, выделяя 6 горизонтальных и 7 вертикальных полос. Также наносим на рисунок оси координат.
Разметка
@gvgs(g,7)@gvvs(g,8)
@gdok(g)
Выводим в верхней области графика названия серий установленным для них цветом, подписи к графикам внизу, а также слева и справа вертикально.
Разметка
@gvos(g,1)@gvct(g,'Funkcii sinus i cosinus',3)
@gvtv(g,'Tekst sleva',1)
@gvtv(g,'Tekst sprava',3)
Графики готовы. Сохраняем в файл и отображаем полученное изображение по центру страницы
Разметка
~f=gsf(g)
@vis(f)
Вывод
Оцените публикацию по предложенной шкале